Efficient modeling and quantification of time-dependent errors in IMPT
PO-1728
Abstract
Efficient modeling and quantification of time-dependent errors in IMPT
Authors: Pia Stammer1,2, Lucas Burigo3, Oliver Jäkel3,4, Martin Frank1, Niklas Wahl2
1Karlsruhe Institute of Technology (KIT), Steinbuch Centre for Computing, Karlsruhe, Germany; 2German Cancer Research Center, Medical Physics in Radiation Oncology, Heidelberg, Germany; 3German Cancer Research Center - DKFZ, Medical Physics in Radiation Oncology, Heidelberg, Germany; 4Heidelberg Ion Beam Therapy Center - HIT, Medical Physics in Radiation Oncology, Heidelberg, Germany
Show Affiliations
Hide Affiliations
Purpose or Objective
Managing uncertainties is a major challenge in IMPT planning, with a continuously growing complexity when not only considering set-up and range errors, but also time-dependent errors such as intrafraction motion or beam application patterns. We introduce an efficient approach to error modeling, which makes use of beamlet correlations to incorporate even complex time dependent error patterns without the need for excessive scenario computations.
Material and Methods
We assume a multivariate Gaussian error model, where each dimension corresponds to the error in an individual beamlet with a Gaussian marginal distribution. The covariance matrix of this multivariate model can reflect the spatial as well as time-dependent (auto-)correlation patterns. Uncertainty quantification methods such as our proposed importance reweighting for MC or analytical probabilistic modeling (APM) for pencil beam dose calculations then allow an efficient quantification of the uncertainties directly from the error model.
We further use the time-dependency inherent in the beam application process to derive covariance matrices representing intrafraction motion interplaying with the beam application pattern. Each beamlet is associated with a point in time during treatment. Previous works have already demonstrated that specific types of intrafraction motion may be modeled as time series using, e.g., random walks, auto-regressive (ARMA) models or Gaussian processes. Due to their recent rise in popularity in ML applications, covariance kernels for a number of such processes are already available in literature.
Results
A covariance matrix for random movement was derived using an AR(1) process, where the displacement in each time step depends on the previous time step as well as an independent random shift. Periodic motion was modeled using a Gaussian process with a local periodic covariance kernel, representing periodically repeated shifts which may change over time.
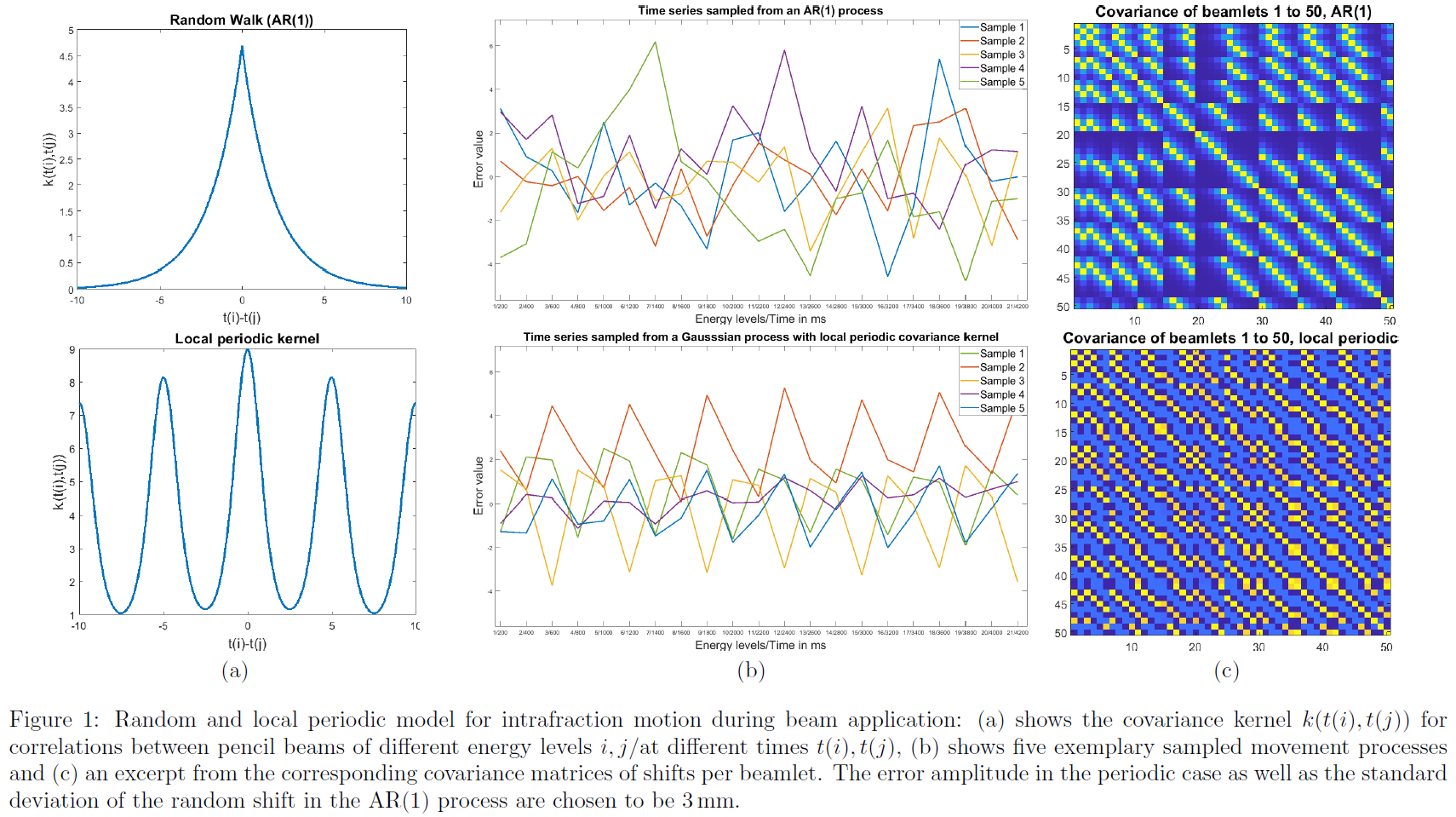
These models were applied for the computation of the dose standard deviation in a liver patient using importance reweighting and compared against a standard set-up error with full beamlet correlations. The computational complexity of uncertainty estimation is greatly reduced compared to a standard scenario-based reference, which would require laborious set-up as well as a large number of error scenarios due to the high dimensionality of the uncertainty space.
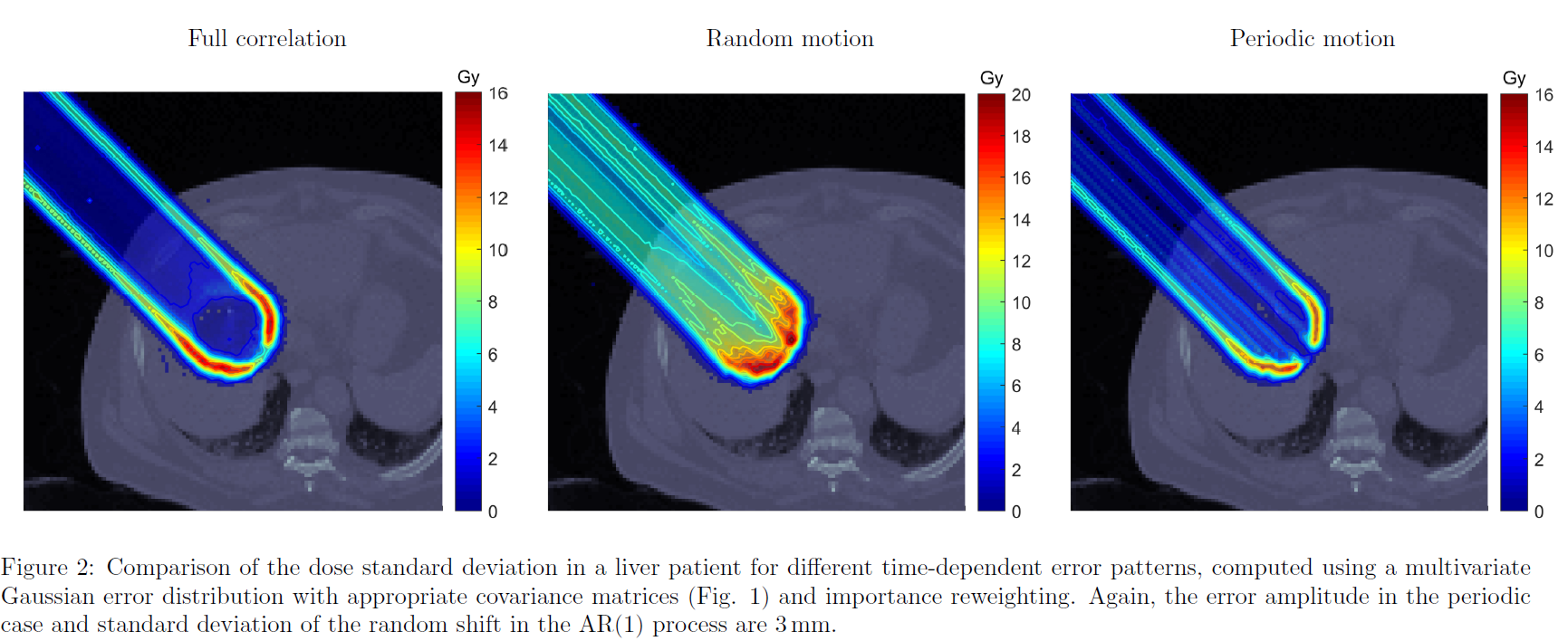
Conclusion
Our results indicate that time-dependent uncertainty during treatment may be captured in multivariate Gaussian error models, using appropriate beamlet (auto-)correlations. We show that random and periodic intrafractional movements may be approximated without the need for 4D computations or a large amount of error scenarios, when combining these models with uncertainty quantification methods such as importance reweighting. In the future, a validation against 4D scenario computations and an extension to models for more realistic errors, e.g., based on observed patient motion, is planned.