Session Item

Currently a constant relative biological effectiveness (RBE) is employed during clinical proton therapy, although it is well known that the RBE is variable depending on linear energy transfer (LET), dose level and tissue. The lack of versatile tools for calculation of the RBE variability is potentially degrading plan quality and preventing fulfillment of high accuracy protons. LET can be obtained using a Monte Carlo (MC), although calibration should be performed to achieve correct values representative for the specific treatment planning system (TPS). This work provides a streamlined method for calibrating range, stopping power, density corrections, relative stopping power and dose for the MC to treatment planning of intensity-modulated proton therapy (IMPT). 

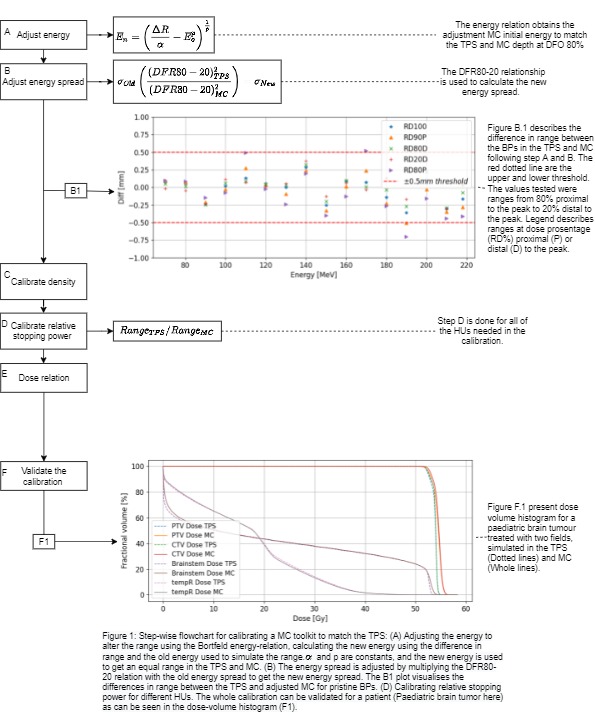
An overview of the stepwise calibration procedure is presented in Fig 1. Pristine Bragg peaks (BPs) were created in 10 MeV intervals in the Eclipse TPS (ProBeam360 data) as well using the FLUKA MC. A phantom with a relative proton stopping power (RPSP)=1 was used for the TPS and set to water for the MC. Subsequently, the MC parameters, initial energy and energy spread were adjusted to fit the TPS: The Bortfeld energy-range relation was rearranged for adjustment to the initial energy of the beam and applied to fine-tune the range of the MC BPs at 80% of the distal dose fall-off (DFO) (Fig 1.A). To modify energy spread, the distal dose fall-off range 80%-20% (DFR80-20) of the pristine BP was calculated for the MC and TPS. The correction factor was decided by dividing the DFR80-20 for the TPS by the MC value (Fig 1.B1). Density corrections for the different materials were calculated based on CT-calibration curves from the TPS (Fig 1.C). Relative stopping power for Hounsfield units (HUs) in the interval -925 to 3069 was calculated by dividing the range at 80% of DFO for the TPS by the MC (Fig 1.D).  Trapezoidal integration was applied to find the relationship between the dose per particle for the MC and dose per monitor unit (MU) in the TPS. 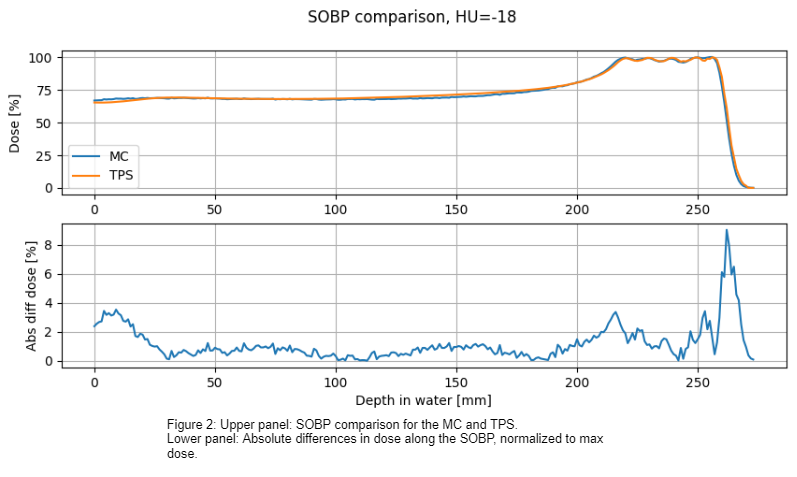The calibration was validated in a spread-out Bragg peak (SOBP) in water and in a 2-field treatment plan of a pediatric brain tumor. 

Differences in both range and energy spread were within +/- 5 mm along the depth curve for different % of the Bragg peak (Figure 1.B.1). The SOBP validation resulted in an absolute mean difference in dose of 1.1% for the whole SOBP (Figure 2), and a maximum of 9% difference in dose for the SOBP. The patient validation resulted in good accuracy between the TPS and MC for all dose levels, with modest differences found in the high dose regions for both target volumes and organs at risk (Fig 1.F1).

An efficient approach for calibrating MC codes to a specific TPS has been presented and achieved good accuracy in range, energy spread, density and stopping power. The procedure can be applied to any specific TPS and IMPT delivery unit as well as measurements, and allows for calculating LET values and subsequently variable RBE.