A review of Monte Carlo calculated fQ factors for ionization chambers in clinical proton beams
Kilian-Simon Baumann,
Germany
PO-1553
Abstract
A review of Monte Carlo calculated fQ factors for ionization chambers in clinical proton beams
Authors: Kilian-Simon Baumann1, Carles Gomà2, Jörg Wulff3, Jana Kretschmer4, Klemens Zink5
1University Medical Center Giessen-Marburg, Department of Radiotherapy and Radiooncology, Marburg, Germany; 2Hospital Clínic de Barcelona, Department of Radiation Oncology, Barcelona, Spain; 3West German Proton Therapy Centre Essen (WPE), Department of Particle Therapy, Essen, Germany; 4Carl-von-Ossietzky University Oldenburg, University Clinic for Medical Radiation Physics, Medical Campus Pius Hospital, Oldenburg, Germany; 5Marburg Ion-Beam Therapy Center, Department of Particle Therapy, Marburg, Germany
Show Affiliations
Hide Affiliations
Purpose or Objective
Currently, the IAEA TRS-398 Code of Practice is being updated. The
updated version will provide values of beam quality correction factors (kQ) for air-filled ionization
chambers in clinical proton beams based on Monte Carlo simulations and
experimental data. In recent years, the Monte Carlo codes PENH, GEANT4 and
FLUKA have been investigated in terms of their feasibility for dosimetric
calculations. It was shown that all three codes can be used to calculate kQ factors to be in agreement
with experimentally determined ones on the 1%-level.
In this study, we review the available data on Monte Carlo calculated fQ factors in clinical proton
beams which enter into Monte Carlo calculated kQ factors. We provide average fQ factors and discuss type-B uncertainties.
Material and Methods
From fQ factors as
published in the literature, weight-averaged fQ factors for different ionization chamber models were
derived. The weight of each fQ factor
was indirectly proportional to its corresponding relative type-A uncertainty. In
general, the amount of available data is not the same for all Monte Carlo
codes. To avoid a code-specific bias, the weight of each fQ factor from one Monte Carlo code was reduced if more
than one value was available in the literature. Subsequently, the weight-averaged
fQ factors as a function
of residual range (Rres) were
fitted with a polynomial function of order 2.
In order to estimate the type-B uncertainty of weight-averaged fQ factors, a rectangular
distribution was assumed. The width of this distribution was defined as the
difference between the largest and smallest fQ
factor enlarged by their corresponding relative type-A uncertainties.
Results
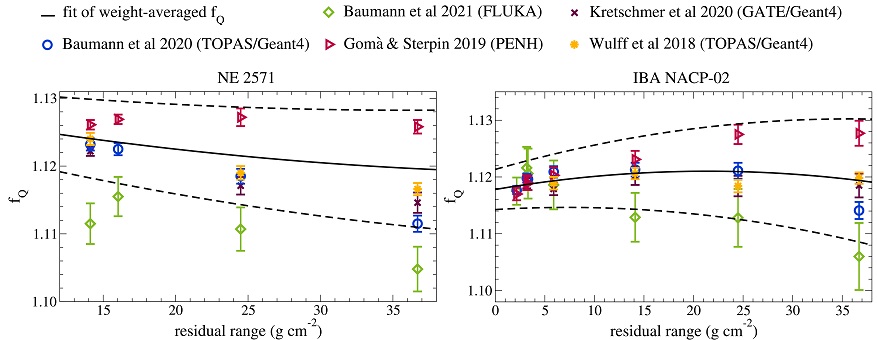
In Figure 1 the fits of weight-averaged fQ factors are shown in solid lines as a function of Rres for an exemplary
cylindrical and plane-parallel ionization chamber. The uncertainty is indicated
as dashed lines. Additionally, the original fQ
factors from the literature are depicted. For the cylindrical chamber fQ decreases by 0.5% with
increasing Rres. For the plane-parallel chamber it is almost
constant with variations of 0.2%.
Additionally, it can be seen that the agreement between the individual
Monte Carlo codes is better for small values of Rres while the codes tend to diverge for larger values
of Rres. Correspondingly,
the uncertainty of weight-averaged fQ
factors increases with Rres
and reach up to 2% (k=1), following the estimation described above.
Conclusion
Weight-averaged fQ factors
were derived from currently published Monte Carlo calculated fQ factors. The Monte Carlo codes show a better agreement for small values of Rres while the codes diverge
for larger values of Rres.
This might be due to differences in the modelling of nuclear interactions whereas
the role of nuclear interactions increases with energy and hence Rres. As a result, overall
uncertainties of Monte Carlo calculated fQ
factors can be expected to be larger for higher energies.