Machine Learning in NTCP prediction --- A superior alternative to the Lyman-Burman-Kutcher model
Pratik Samant,
United Kingdom
PO-1755
Abstract
Machine Learning in NTCP prediction --- A superior alternative to the Lyman-Burman-Kutcher model
Authors: Pratik Samant1,2, Tim Maughan2, Frank Van Den Heuvel3,2, Richard Canters4, Frank Hoebers5, Emma Hall6, Chris Nutting7, Dirk de Ruysscher8
1Oxford University Hospitals NHS Foundation Trust, Radiotherapy Physics, Oxford, United Kingdom; 2University of Oxford, Department of Oncology, Oxford, United Kingdom; 3Zuidwest Radiotherapeutisch Instituut , Physics, Vlissingen, The Netherlands; 4Maastricht University Medical Centre, Department of Radiation Oncology (Maastro), Maastricht, The Netherlands; 5 Maastricht University Medical Centre, Department of Radiation Oncology (Maastro), Maastricht , The Netherlands; 6Institute of Cancer Research, Division of Clinical Studies, Sutton, United Kingdom; 7Institute of Cancer Research, Division of Radiotherapy and Imaging, Sutton, United Kingdom; 8Maastricht University Medical Centre, Department of Radiation Oncology (Maastro) , Maastricht , The Netherlands
Show Affiliations
Hide Affiliations
Purpose or Objective
A popular Normal tissue Complication (NTCP) model deployed
to predict radiotherapy (RT) toxicity is the Lyman-Burman Kutcher (LKB) model
of tissue complication. This model consists of three parameters, n, m, and D50, such
that
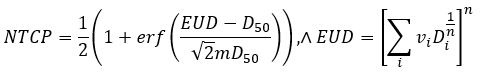
Where vi and Di are the
relative volume fractions and corresponding dose bins of the differential dose
volume histogram (DVH) of an organ. Despite its common use, the LKB
model has some limitations preventing clinical deployment: 1) it can only
consider dose to a single contoured structure 2) it can be numerically unstable
during fitting 3) it is difficult to correct for batch effects.
In this study we examine the ability of the LKB model to predict
Grade 2 Xerostomia in head and neck cancer patients. We also compare LKB
performance to conventional machine learning (ML) algorithms such as logistic
regression (LG), AdaBoost (AB), Decision Trees (DT), and Gradient Boost (GB).
Material and Methods
We acquired parotid gland DVHs and demographic data (gender,
age) from the Outcome
H&N trial to act as the training set. Similarly, the same data of the PARSPORT
trial to act as a test set.
An LKB model to predict G2 Xerostomia was fit on the
training DVHs (constructed by inferring the DVH on extracted metrics), by
varying parameters to maximize log-likelihood after an initial guess. The
model was then evaluated on the test set and the area under the receiver
operating curve characteristic curve (ROC-auc) was used as a metric. Several
initial parameter guesses were tried in accordance with results from Burman et al.
to test for convergence. The model fit was tried using both bounded and
unbounded parameters. Similarly, AB, LG, DT, and GB models were also fit on the
training set and their hyperparameters tuned, using patient dose metrics as
features for fitting.
Results
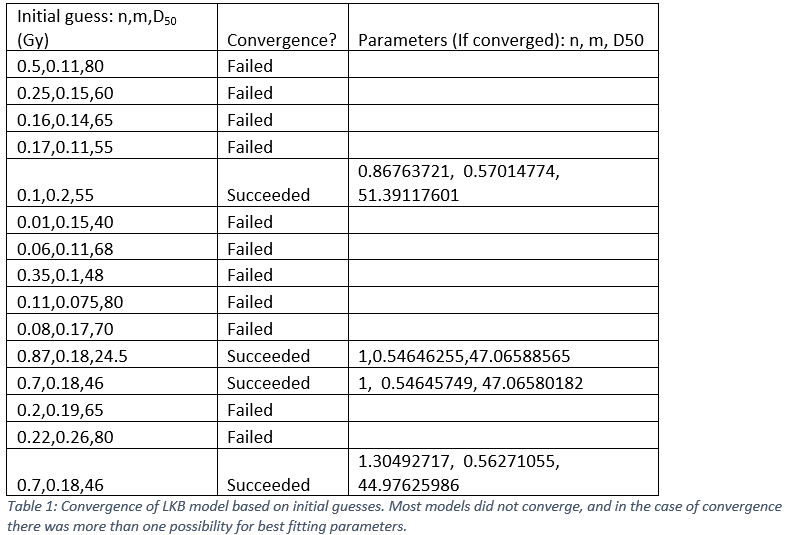
Initial guesses for n, m, and D50 were loosely
chosen based on values provided by Burman et al. for
various organs. The results are summarized in Table 1.
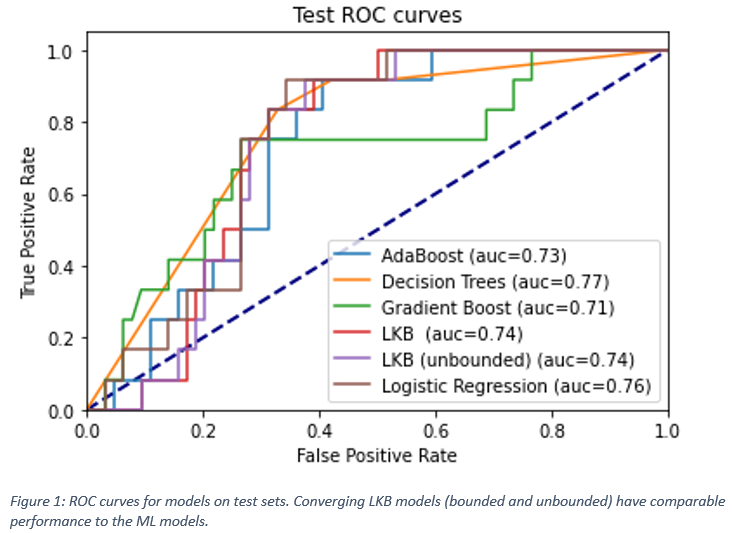
The predictive performance of the models is
summarized below in Figure 1. The converging LKB model using initial guesses of
0.7,0.18,46 (corresponding to parotid values)
was compared with the performance of the ML models. As can be seen, ML performs
comparably to the LKB model even when the latter converges.
Conclusion
Our results show that ML algorithms outperform the LKB model
in most cases, as they always converge and have good predictive capability. This
is even though G2 xerostomia, largely dependent on the dose to the parotid
gland (a parallel organ), is quite a well-suited situation for LKB modelling.
ML models are simple to deploy with modern toolboxes and they have the
additional benefit of being able to consider any features of interest that can
contribute to patient toxicity. Further studies where these models are compared
with LKB performance are needed, particularly in cases where the structure of
interest has both serial and parallel components (e.g. the heart).