Develop a fast spot sparsity optimization algorithm for proton arc therapy
PO-1989
Abstract
Develop a fast spot sparsity optimization algorithm for proton arc therapy
Authors: Xuanfeng Ding1, Lewei Zhao1, Juntao You2, Gang Liu3, Sohpie Wuyckens4, Xiliang Lu5
1Corewell Health William Beaumont University hospital, Radiation Oncology, Royal Oak, USA; 2, The Hong Kong University of Science and Technology, Department of Mathematics, Hongkong, China; 3Huazhong University of Science and Technology, 3Cancer Center, Union Hospital, Tongji Medical College, Wuhan, China; 4UCLouvain, 4Molecular Imaging, Radiotherapy and Oncology (MIRO), Louvain-la-Neuve, Belgium; 5Wuhan University, School of Mathematics and Statistics, Wuhan, China
Show Affiliations
Hide Affiliations
Purpose or Objective
We developed a primal dual active set with continuation (PDASC) for a fast spot sparsity optimization algorithm by reducing the computation time compared to the previous framework on alternating direction method of multipliers (ADMM) for spot-scanning proton arc (SPArc) therapy.
Material and Methods
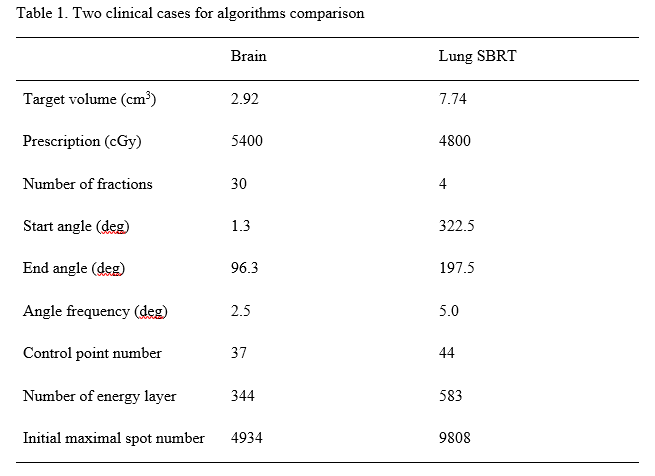
Based on machine-specific beam delivery sequence model of IBA’s ProtetusONE® proton system in Beaumont Proton Therapy Center, beam delivery time is approximately proportional to spot number. Then we propose a l0 -norm sparsity optimization formulation to reduce the spot number. Sparsity level can be controlled by adjusting l0 -norm coefficient. PDASC was developed to search for the spot sparsity solution in this non-convex optimization problem. Our previous work on the ADMM optimization framework was used as a benchmark. PDASC couples the primal dual active set with a continuation strategy on the regularization parameter in outer iteration. Each inner iteration first identifies the active set from both primal and dual variables, then updates the primal variable by solving a (typically small) least-squares problem defined on the active set, from which the dual variable can be updated explicitly.We compare these two algorithms on a brain and a lung SBRT case (Table 1). All simulations of clinical cases were run with the same server hardware. We compare two algorithms on l2 -norm value of plan quality and optimization time for different sparsity levels.
Results
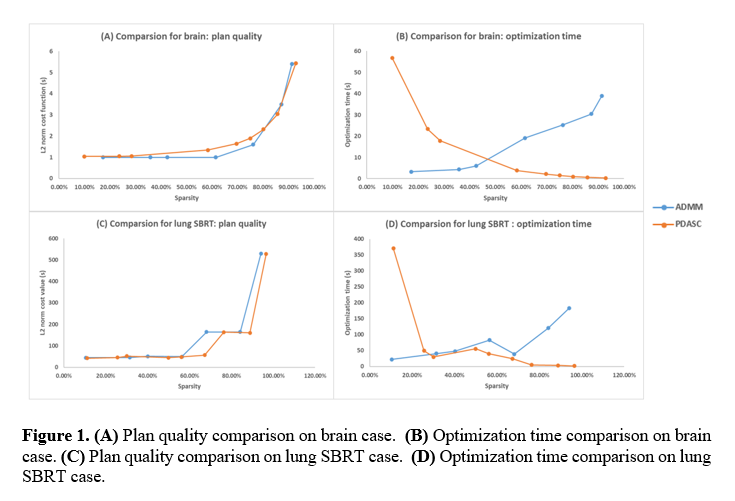
Through the parameter and iteration-stopping criterion adjusting, PDASC and ADMM can reach comparable plan quality (Figure 1A and 1C). Both algorithms showed the trend that the higher the sparsity, the lower the plan quality. When PDASC and ADMM reach similar plan quality, PDASC takes a shorter time searching higher sparsity solutions, and ADMM spends less than finding low-sparsity solutions. For example, the plan quality will get worse as sparsity increased and sharply changes around 90%-100% sparsity level. The higher the sparsity, the shorter the optimization time PDASC use; the lower the sparsity, the less optimization time ADMM spends (Figure 1B and 1D). For the brain case, when sparsity is greater than about 50%, PDASC uses shorter optimization time. For the lung SBRT case, when sparsity is greater than about 30%, PDASC spends less optimization time. Their optimization time difference will significantly increase when sparsity tends to 0 or 100%.
Conclusion
PDASC demonstrated its computation efficiency in the high-sparsity solutions, in which SPArc treatment delivery efficiency is a high priority in the proton routine clinical practice.