Session Item

Proton arc therapy (PAT) is a new delivery technique that exploits the continuous rotation of the gantry to distribute the therapeutic dose over many angular  windows instead of using a few static fields, as in conventional (intensity-modulated) proton therapy. Although coming along with many potential clinical and dosimetric benefits, PAT has also raised a new optimization challenge. In addition to the dosimetric goals, the beam  delivery time (BDT) needs to be considered in the objective function. Considering this bi-objective formulation, finding a good compromise with appropriate weighting factors turns out to be cumbersome. The goal of this study is to demonstrate the feasibility of applying a bi-criteria optimization (BCO) algorithm to a restated PAT problem, to investigate the trade-offs between the plan quality and the delivery time.

The BCO algorithm computes a database of Pareto-optimal plans, i.e., treatment plans for which no other better plan exists in every measurable dimension. We have implemented the BCO algorithm in an in-house treatment plan system, OpenTPS, and computed Pareto-optimal arc plans for three disease sites: a brain, a lung, and a liver. The method iteratively picks weight vectors to approximate the Pareto front with few points. Mixed-Integer Programming was selected to restate PAT as a bi-criteria problem and to find Pareto optimal points with a suited solver.

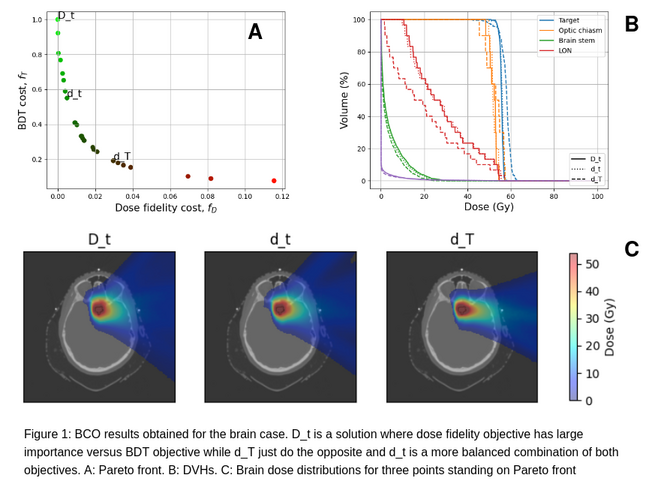
For each patient, the Pareto frontier is approximated by a set of Pareto-optimal points (Figure 1a, brain case). Next, the trade-offs between plan quality and beam irradiation time (static BDT) are investigated by inspecting three plans from the Pareto front. The latter are carefully picked to demonstrate significant differences in dose distribution (Figure 1c, brain case) and delivery time depending on their location on the frontier as reported in the table (Table 1) and in the dose-volume histograms (Figure 1b). The first point D_t brings the plan with the highest quality but the largest irradiation time while the point d_T does the complete opposite. Finally the intermediate point d_t shows a better compromise between both objectives, losing 1Gy in target coverage but reducing by almost 50% the irradiation time for the brain case. However, this point was only picked to demonstrate the potential of BCO for PAT, the task of finding the best compromise remains a clinical decision.

Table 1: Summary of optimization results for the brain case for three points standing on Pareto front

This study introduces the application of BCO to the PAT problem, which eventually permits the planners to select the best treatment strategy according to their own preferences.