Session Item

Inconsistencies in dose delivered during carbon radiotherapy is due largely to uncertainties in RBE, which is calculated using one of several models that typically require Monte Carlo computed input parameters. While RBE by Microdosimetric Kinetic Model (MKM) can be calculated using a measured microdosimetric values, there exist no direct means of measuring RBE by other common models, including Repair Misrepair Fixation (RMF) and Local Effect Model I (LEM). This study investigates estimating RBE using a uniform, microdosimetric measurement for each model, allowing measurement-based validation of model implementation and RBE comparison across models and institutions.

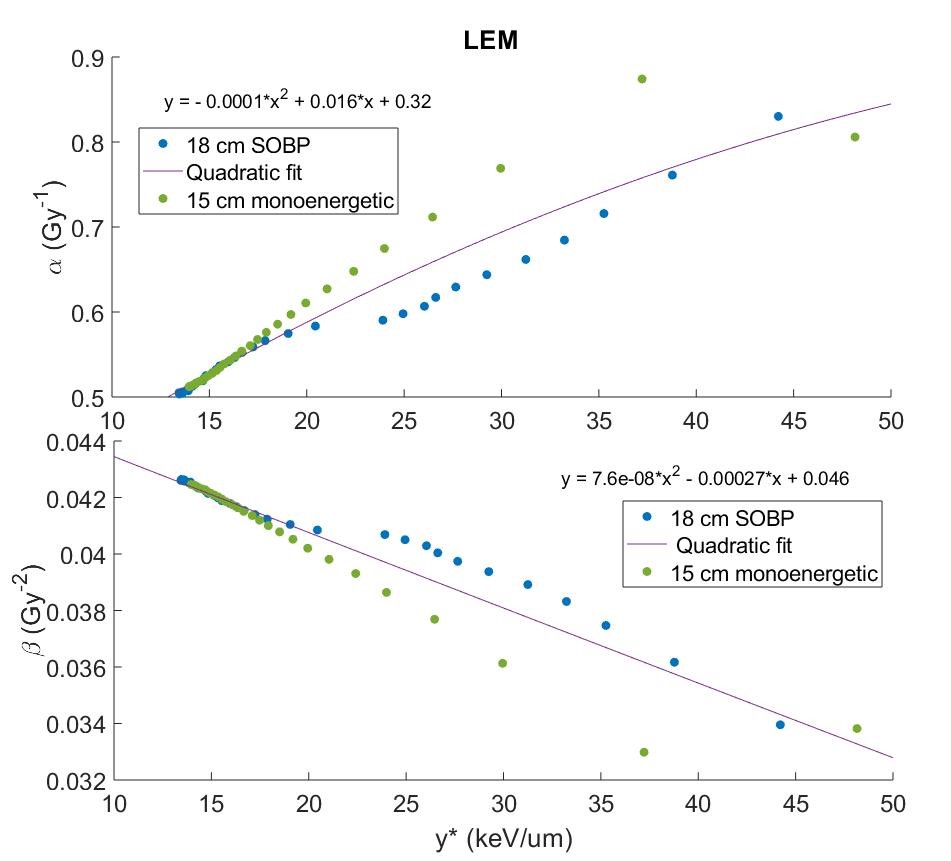
Monte Carlo simulations were used to calculate the biophysical properties of carbon ions that serve as RBE input parameters: microdosimetric quantities, double-strand break yields, and kinetic energy distributions for 10 clinically realistic carbon beams (7 monoenergetic/3 SOBP). For each MKM, RMF, and LEM, we calculated particle α and β, and subsequent RBE according to model definitions using proper input parameters.  Next, model-specific particle α and β values from two beams were plotted as a function of the corresponding positional microdosimetric value, y*, as scored within a TEPC to represent a case for which the input had just been measured, and fit with a polynomial (example in Figure 1). This fit was used to estimate particle α and β for remaining beams to validate the robustness of the fit. The percent difference between true RBE and RBE calculated with TEPC-simulated y* was calculated to quantify the uncertainty in this measurement-based approach to estimating RBE. A ±5% threshold was selected to determine acceptability.

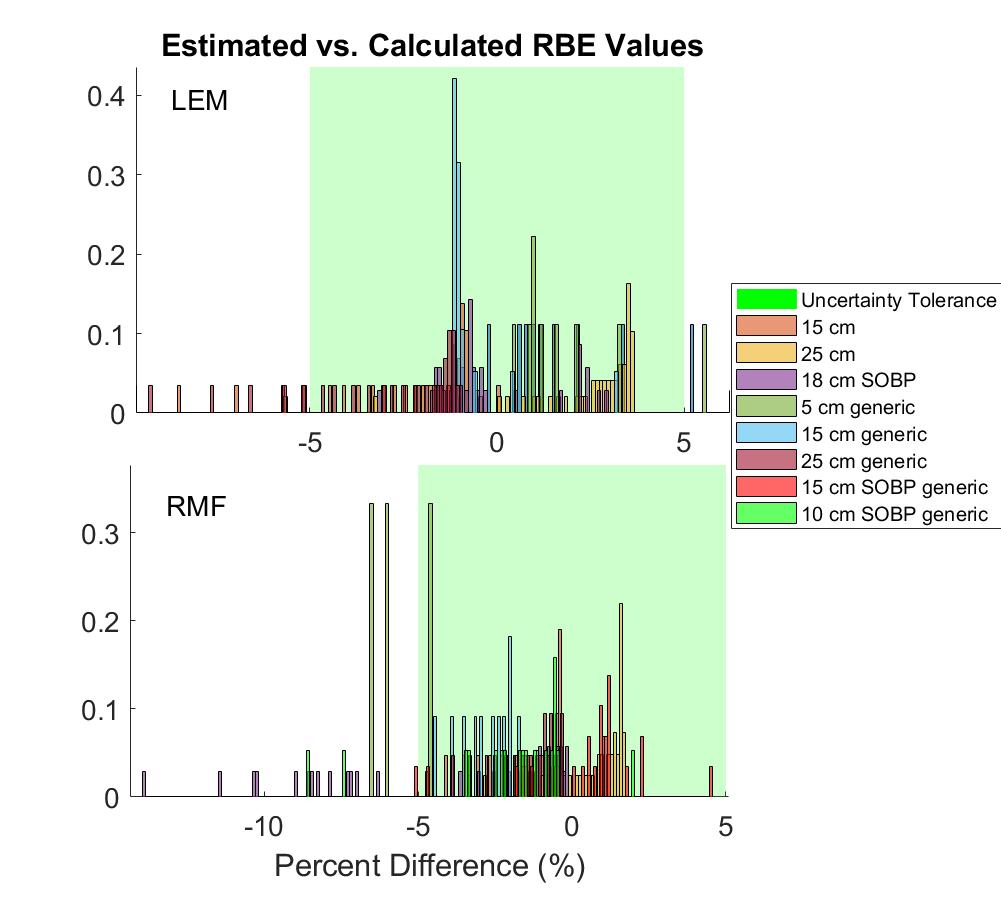
The estimation method had a ±5% accuracy in 91% of data points across all beams and all three models. A histogram of estimation accuracy is shown in Figure 2 for RMF and LEM. For all models, accuracy in the entrance region was typically <1%, while greatest error was seen in areas of rapidly changing physical dose and LET (just proximal to Bragg peak/SOBP). This was tolerable, particularly in a clinical audit framework, as these regions are already areas of high dosimetric uncertainty. The effect of physical dose on the estimation method was also evaluated, and increases in dose were found to notably improve accuracy.

To establish a common framework within which RBE estimated using each model can be directly measured, we designed microdosimetric estimation methods for each model based on a single measurable input, which were almost always able to predict true RBE to within ±5% accuracy. Based on the results of this study, evaluation of the modeled RBE value based on microdosimetric measurements, is reasonable. This work provides a framework for an intercomparison system, which will be capable of delivering measurement-based feedback on the clinical implementation of RBE models to allow for practical comparison of RBE across both institutions and models.