Session Item

The gamma test is a quantitative method to evaluate the differences between the dose distribution to be delivered to the patient during treatment versus the dose distribution obtained in the treatment planning system.
The aim of this work is to develop a Machine Learning model to predict whether a planned treatment will pass or fail the test, without having to deliver it over a matrix of detectors in the treatment unit.

A total of 198 treatments were analysed, 128 of which were delivered on the ArcCheck model 1220 detector array, analysing the 3%/3mm and 2%/2mm parameters of the gamma test. The remaining 70 treatments were delivered on the SRS MapCheck model 1179 detector array, placed on the StereoPHAN phantom, analysing the 3%/1mm and 2%/1mm parameters of the gamma test.
The work has been carried out using the scikit-learn library in Python 3.9.13, with the following supervised learning methods for regression: linear regression, support vector machine (linear, degree 2 polynomial, degree 3 polynomial and radial basis function (RBF) kernels) and decision tree.
The training and validation has been performed by K-fold Cross-Validation (10 folds) using 90% of the treatments, rescaling and analysing the following complexity parameters: Mean Gap (average MLC gap in mm), Q1 Gap (first quartile of the MLC GAP), Mean TGi (mean Tongue and Groove index), TGi Ratio (ratio between MeanTGi and Mean Gap), Mean MLC Speed (mean speed of all in-field leaves (cm/s)), MLC Speed Mod (Mean variation of MLC speeds), Mean GS (mean Gantry Speed (deg/s)), GS Modulation (total Gantry Speed  variation), Mean RR (mean Dose Rate (MU/min)) and RR modulation (total Dose Rate variation).
The remaining 10% of the data has been used to test the models with lower RMSE.

After training the regression models, the lowest RMSE values are obtained for the depth 5-decision tree for 3%/3mm, the depth 2-decision tree for 2%/2mm and the support vector machine with RBF kernel for 3%/1mm and 2%/1mm. The obtained results are shown in table 1.

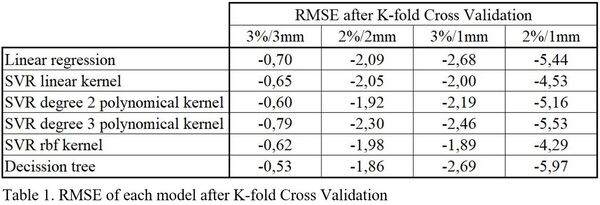
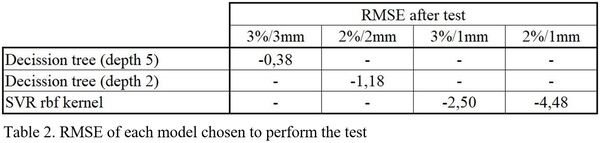
In the test phase, the RMSE values obtained for the models that obtained the best training values are 0.38 for 3%/3mm, 1.18 for 2%/2mm, 2.50 for 3%/1mm and 4.48 for 2%/1mm. The results are shown in table 2.

The models obtained are sufficiently good to constitute a first filter after planning, allowing us to estimate the gamma test and make corrections in the planning to reduce complexity if necessary, but in no case they can replace the measurements made by an array of detectors in the treatment unit.