Session Item

The shape of the energy spectrum is an essential component of any electron beam Monte Carlo model. Due to specialized equipment and the long measurement time for the direct methods for determining the energy spectrum, attractive alternatives are backward spectrum reconstructions from the measured data. One such approach is solving the first-degree Fredholm integral equation with appropriate regularization. Thanks to this, it is possible to calculate the depth distribution as the sum of the distributions from monoenergetic beams. This study aims to determine the optimal value of the regularization parameter for the problem of determining the spectrum of the electron beam produced by a mobile accelerator used during intraoperative radiotherapy.

The study was carried out with the use of MC simulation methods. The Geant4 package was used to generate the distributions of deep doses for monoenergetic beams for two models with different degrees of complexity, i.e. simple (theoretical) and full (for the mobile accelerator) (Figure 1). The dose distributions for four different shapes of energy spectrum (for each model) were obtained similarly. They were established as the reference data for further calculations. The Dual Annealing optimization method was used to obtain the reconstructed spectrum. The multiple optimizations that differ by the regularization parameter (ranging from 0 to 1) were performed. For each reconstruction, similarity indicators of the energy spectrum and the dose distribution to the referenced data were calculated to determine the optimal regularization parameters.

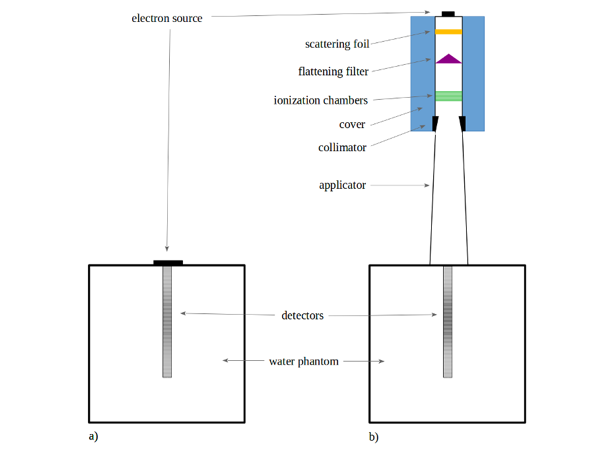
Figure 1. Geometry of the simulated system: a) maximally simplified geometry consisting of an electron source and detectors placed in a water phantom (hereinafter referred to as simple); b) extended geometry with all elements of the accelerator head (hereinafter referred to as full), simplified drawing, no scale.

Optimal regularization parameters determined based on similarity indicators for the spectrum and the dose distribution differ for geometry models considered in the study. The regularization parameter for the simple geometry ranged from 0.03 to 0.05, while for full geometry, they were from 0.05 to 0.06. The results for conventional linear accelerators found in the literature range from 0.5 to 1.1.

The Dual Annealing optimization method can be effectively used to solve the Fredholm equation with Tikhonov regularization to reconstruct an electron beam's energy spectrum. The regularization parameter value depends on the beam-forming system. Its value for the mobile accelerator considered in the study ranges from 0.05 to 0.06, depending on the nominal beam energy value (Figure 2).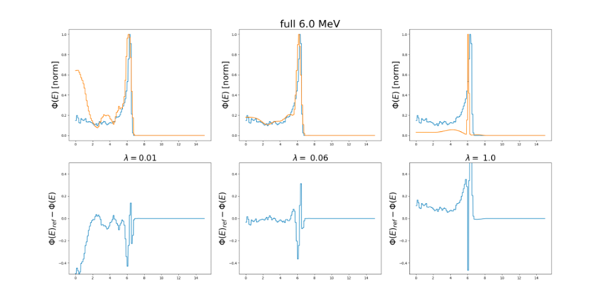

Figure 2. An example of comparison of the reconstructed (orange) and reference (blue) spectrum for the geometry with all the elements of the machine (full geometry) for a nominal energy of 6 MeV for the three values of the regularization parameter λ. The lower charts show the difference.