Purpose and background
To address the limited availability of radiation shielding data for brachytherapy as well as some disparity in existing data, Monte Carlo simulation was used to generate radiation transmission data for 60Co, 137Cs, 198Au, 192Ir, 169Yb, 170Tm, 131Cs, 125I and 103Pd photons through concrete, stainless steel, lead, as well as lead glass and barite concrete. This data can be easily and accurately used for shielding design purposes using the values of a three-parameter empirical fit that are also provided for every radionuclide-material combination. This work is extensively described in a paper published in Medical Physics (2008) [1], including details of the MC simulation as well as a comparison with previous results in the literature [2-5].In addition to the material published in this paper, the present web pages can be and will be further updated to include information on other brachytherapy radionuclides and other shielding materials aiming at providing a useful and comprehensive set of data for brachytherapy facility shielding.
Monte Carlo code
The GEANT4 code v.7 was employed for MC simulations in this work using the EPDL97 cross section libraries. The MCNPX code v. 2.4.0 was also used in simulations for selected radionuclide-material combinations as an independent check. Results of the two codes were found in close agreement and results presented here correspond to the GEANT4 simulations.
Monte Carlo geometry
The simulation geometry is shown on this page and comprised an air filled box of x×y×z = 5×5×3 m3dimensions with the source of a chosen radionuclide centred on the yz plane at x=0 and a barrier of given material and thickness ∆x positioned with its distal surface to the source at x=1 m. The same geometry was used for all radionuclide-shielding material combinations with photons emitted isotropically in a 2π solid angle towards the barrier to simulate broad beam conditions in a realistic geometry. Transmission was scored 30 cm behind the barrier which is consistent with the practise of NCRP Reports [5, 6]. The percentage elemental composition and density of all materials are presented in Table I of the original work.
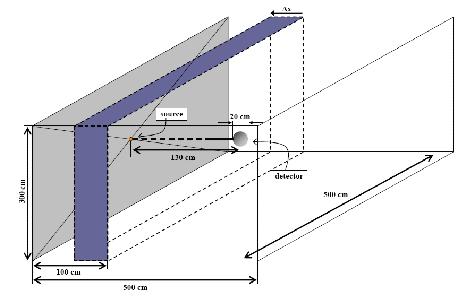
Source description
Bare point sources were simulated for each of the radionuclides studied in this work. The emitted photon spectrum of the radionuclides was taken by NuDat 2.4, excluding photon lines of energy lower than 10 keV that would be strongly absorbed by the core and encapsulation of real source designs. It must be noted that bremsstrahlung production due to the beta emissions of 170Tm was not taken into account. This latter decision was taken as no construction details of a source containing 170Tm were known to the authors. For a real source design with 170Tm this calculation should be repeated.
Presentation of the data
Results are shown in the form of tables with the numerical data of each combination of radionuclide and shielding material.
These tables include the thickness of the shielding material, the transmission factor, the estimated uncertainty and the outcome of a 3-parameter fitted model of each combination.
A graphical presentation in four decades of the transmission factor is directly available for each combination of radionuclide and shielding material, obtained by selection of the desired combination.
Fitting procedure
The three-parameter model introduced by Archer et al (1983) [7] to facilitate diagnostic x-ray shielding calculations was used to describe transmission results of this study. The equation of this model has the form:
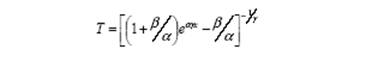
where T stands for transmission, x is the thickness of the shielding barrier (denoted by ∆x in the description of the simulation geometry in the previous section) and α, β, γ are constant terms to be determined by the fit and depend on photon energy as well as the barrier material. The barrier thickness to achieve a given transmission can be calculated by solving this equation for x which yields:
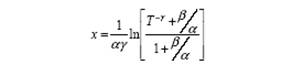
At large barrier thickness, x, transmission tends to exp(-αx) according to the first equation and α is the slope of the transmission curve beyond the depth where the relative directional and energy photon distributions are almost independent of thickness. Here, equilibrium HVL and TVL values, HVLe and TVLe, can be calculated as ln2/α and ln10/α, respectively.
Materials
Click on the materials to find transmission data for all radionuclides:
Acknowledgements
The work described in this paper was performed within the framework of the GEC-ESTRO working group BRAPHYQS working group (BRAchytherapy PHYsics Quality assurance System) physicists’ network. BRAPHYQS members are deeply acknowledged for their contributions to the discussions on this topic. Companies supporting the meetings of BRAPHYQS are acknowledged for their financial support: Oncura, Varian, and Nucletron.
References
For a more complete list >>>
-
P. Papagiannis, D. Baltas, D. Granero, J. Pérez-Calatayud, J. Gimeno, F. Ballester, J. L. M. Venselaar. “Radiation transmission data for radionuclides and materials relevant to brachytherapy facility shielding”. Med. Phys. Vol. 35 (11), November 2008 4898-4906
-
NCRP (National Council on Radiological Protection and Measurements) 1976. “Structural Shielding Design and Evaluation for Medical Use of X Rays and Gamma Rays of up to 10 MeV”. NCRP Report No. 49 (Washington, DC: NCRP).
-
D. Delacroix, J. P. Guerre, P. Leblanc, and C. Hickman. “Radionuclide and Radiation Protection Data Handbook”. Rad. Prot. Dos. 98, 1–168 (2002).
-
IAEA (International Atomic Energy Agency) 2006. “Radiation Protection in the Design of Radiotherapy Facilities”. Safety Reports Series No. 47 (Vienna: IAEA).
-
NCRP (National Council on Radiological Protection and Measurements) (2005). “Structural shielding design and evaluation for megavoltage X- and gamma-ray radiotherapy facilities”. NCRP Report No. 151 (Washington, DC: NCRP).
-
NCRP (National Council on Radiological Protection and Measurements) 2007. “Management of Radionuclide Therapy Patients”. NCRP Report No. 155 (Washington, 360 DC: NCRP).
-
B.J. Archer, J.I. Thornby, and S.C. Bushong. “Diagnostic x-ray shielding design based on an empirical model of photon attenuation”. Health Phys. 44, 507–517 (1983).